
周期中的其他文章
在本IV部分中,我们完成了对AES-128密码的描述。对于不熟悉本书前几部分的读者,我将说明该材料是出于教育目的而提供的,它具有许多功能(详细信息,数值示例,数学基础等),而不仅仅是为了使自己熟悉该标准。 ,以及在加密和解密算法(没有密钥的情况下)的开发中使用的材料。许多知名的在线(和离线)出版物的作者并没有设定自己的目标,这使得这些出版物对我们的目的没有多大用处。
加密的反向过程称为消息解密。为了解密(使用密钥)密文(PCT),创建了一个反向替换表和一个循环密钥,它们相对于加密方案以相反的顺序使用,但类似于加密过程。
解密AES消息
解密消息的操作列表与加密相同。有关操作的更多详细信息,请参见此处。这是密码的相当普遍的原理-用于加密和解密的单个硬件实现,由两个过程的一组相同功能提供。仅源文本和密钥提交顺序被更改。
解密消息的过程实现为用于加密的一系列反向(逆向)转换,在加密过程中按相反顺序进行。同样明显的是,按适当的顺序使用了回合密钥:首先,最后接收到的密钥,然后是倒数第二个密钥,依此类推,直到第一个回合密钥为止。
所有转换名称均保持不变,但以Inv为前缀。我们将按照与以前相同的顺序来考虑它们。AES密码允许两个解密选项,即反向和正向,下面将详细讨论。
反向解密选项
消息的反向解密是逆向加密过程的自然过程。
对于状态的所有16个字节,AddRoundKey操作与加密消息时所做的操作相同(未更改)S + Ki。是它本身的逆。这是由于在操作中使用了XOR逻辑,并且字节以二进制数字表示。
只需将最后一轮的密钥添加(汇总)到加密的消息中即可。
InvSubBytes。这种转换的本质没有改变,即正在转换的消息的每个字节都被替换为表中的另一个字节(S -1-block)替换。当然,替换表在这里是不同的。根据相同的原理,将字节{x,y}替换为Inv S(x,y)中的字节:x-表行,y-其列。从Inv S(x,y)表的行(x)和列(y)的交点处的单元格中获取替换字节。
如前所述,表的大小为16×16 = 256字节,每个字节都是通过向量矩阵乘法和减法(仿射变换)从移位向量C的乘积获得的。在二进制字段中,加法和减法运算是等效的,因此向量C可以简单地加到产品。 InvSubBytes表如下所示。下表1中列出了指定的替换S -1节点,以十六进制格式给出了值:
表1.反向S -1-块的替换表

该表显示了替换为绿色的两个字节4A→5C和9F→6E的示例。
InvShiftRows。此转换将表中的行(状态方块)向右移动(与原始移动相反的方向)。每行的移位值保持不变:第一行(顶部)没有移位c0 = 0,第二行移位了c1 = 1,下一行移位了c2 = 2,最后一行移位了c3 = 3个位置(像元)。表格cc,c1,c2,c3的值已在表和上图中给出,用于第一轮消息转换。

这种在标量表示形式中相乘的结果为:
S'0C =({0l}·S0C){({0b}·S1C)⊕({0d}·S2C)⊕({09}·S3C);
S'1C =({09} S0C)⊕({0l} S1C)⊕({0b} S2C)⊕({0d} S3C);
S'2C =({0d} S0C)⊕({09} S1C)⊕({0l} S2C)⊕({0b} S3C);
S'3C =({0b} S0C)⊕({0d} S1C)⊕({09} S2C)⊕({0l} S3C)。
为了从PC获得IT,解密算法使用与加密过程中相同的参数值。对于扩展密钥的形成,规则保持不变。
直接解密选项
解密算法的特殊性使一些逆变换可以保留与加密算法中相同的操作序列,但是某些参数值需要更改。首先,我们在谈论密钥(它的展开)。
研究表明,SubBytes()和ShiftRows()函数的顺序不会更改结果的值,也就是说,这些函数是可置换的(它们可以上下班)。此位置(属性)对于函数InvSubBytes(),InvShiftRows()也适用。这种模式很容易解释。关键是这两个函数都对整数字节进行操作,并且移位由字节的整数倍执行,并且不会更改字节本身的值。
请注意以下有关MixColumns()的操作。它与输入字节(数据)成线性关系。
InvMixColumns(状态XOR圆形键)= InvMixColumns(状态)XOR
InvMixColumns(圆形键)。
函数(属性)的这些功能允许更改其应用程序的顺序,即
InvSubBytes(InvShiftRows())= InvShiftRows(InvSubBytes())。
AddRoundKey(InvMixColumns())= InvMixColumns(AddRoundKey()),
但前提是扩展解密密钥的列(32位字)先前已通过
InvMixColumns()函数传递。
前述意味着通过保留使用加密所采用的功能的顺序,可以使PC的解密方式有效。显然,在这种情况下,大大降低了密码的硬件和软件实现成本。所做的更改仅涉及生成密钥部署的过程。
在InvMixColumns()函数中,您需要转换变量的类型,该函数的输入参数是二维字节数组(正方形),而扩展键形成为32位字的线性(字符串)数组。因此,必须对正方形进行类型匹配。
让我们使用2轮转换的示例展示RIJNDAEL解密过程的两个等效版本。第一个选项是加密函数的通常逆函数。通过在三对转换
InvShi ftRows()→InvSubBytes()2次和
AddRoundKey()→InvMixColumns()1次中进行三对转换,可以从第一个选项获得第二个选项。
从原始对转换为
指定对中的反向操作序列时,将保存转换结果。
从表中我们可以看到,加密过程和解密过程的第二种变体在使用回合密钥(执行AddRoundKey操作时),替换表(执行SubBytes()和InvSubBytes()操作时)和转换矩阵(执行MixColumns( )和InvMixColumns())。
表2-RIJNDAEL的两轮版本中的转换序列

事实证明,对于任何数量的轮次,都是如此。
使用最后一个子密钥恢复密码密钥
生成圆形AES密码密钥。从128位原始密码密钥生成轮密钥的密钥时间表是递归函数。该功能在详细讨论这里。启动它的初始条件是密钥的前4个4字节字(4×32位字),即W [0],W [1],W [2],W [3]。
让我们将恢复该128位密码密钥的问题公式化如下:找出第10个回合密钥W [43],W [42],W [41],W [40]的组件。
只需要使用此回合密钥来恢复完整的密码密钥。
首先在数值数据上考虑解决问题的方法很方便。让我们以FIPS PUB 197中给出的数值示例为基础。。表3包含第10回合密钥。
生成圆形密钥的过程的组织方式使得它可以沿多个先前的密钥值向前移动(密钥的展开)。为了从一系列值的某个点向后移动,必须在此返回点具有计算过程的初始数据。令返回点为最后一个第10轮的最后一步,即,第10轮的四个4字节字Nk = Nb = 4
表3-AES密码的第10轮的128位密钥

此外,密钥恢复算法的结果和作用用于为方便起见,将其放入表4中,该表类似于(某种形式的)密钥生成表。
表4-从第十轮已知密钥中恢复密码密钥

表4的说明。从10号到1号以相反的顺序计算轮数。该表的三列(3、8、9)包含现成的键,这些键具有不同的当前编号,具体取决于i行号。其余单元格包含用于中间计算的辅助数据。因此,键W [i]的值在表中的三列中出现了三次。
第1栏和第2栏是回合的数字r和4字节关键字的序数i。加密过程中最后一个这样的单词的编号为i =43。在表中,我们将其写在右(9)列的顶行。表的i行号在减少,在第9列中它们对应于关键字W [i]的单词。第8列包含键的单词W [i-Nk],且其数量减少为W [43-4] = W [39],而第3列-关键字W [i-1] = W [42],先前的W [i] = W [43]。
第八列中的单词W [39]的含义未知,我们可以使用公式从原始数据中找到它:
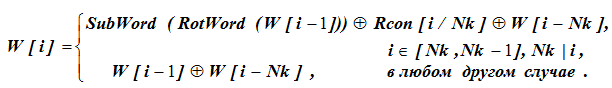
对于公式计算,首先检查选择公式行的条件。对于W [43],i = 43,而Nk并未完全除以值43,也就是说,对于i = 43,W [i]的值由以下公式的底线确定:W [43] = W [42] W [39]。在此,对于W [42]和W [43]的给定值,未定义最后一项W [39]。
那么W [39] = W [43] W [42] = b6630ca6-e13f0cc8。
在二进制算术mod2中,加法和减法运算是等效的,因此,关键字W [39]的4个字节中的每个字节的按位计算采用以下形式(表5):
表5-关键字W [39]的字节计算。

因此,找到了关键字W [39] = 575c006e的值。我们将此值传输到第3列,第i = 40行和第9列到i = 39
行。i = 40行的计算与扩展键时相同。
必须像前面的情况一样,通过行40的差W [36] = W [40] 7列来确定未知单词W [i-Nk] = W [40 –Nk] = W [i = 36]
。第40行的第4列形成为第5列和第6列的总和(OR)。在RotWord循环移位(第4列)和SubWord替换操作(第5列)之后,从W [39]获得第5列值。
这些操作的结果的形式为
RotWord(575c006e)= 5c006e57;子字(5c006e57)= 4a639f5b。
第六列中的值作为常数获得
Rcon [j = i / Nk] = Rcon [j = 40/4] = 2j -1= 2 9。
该常数是由十六进制字节表示
2 9 ≈100000000= X 9,但不存在这样的字节在GF(2 8)字段:您需要通过一个不可约多项式,即找到除法的余
在关键字中包含常量之后,我们得到
Rcon [j = 40 / Nk] = 36000000(第6列)。以(7列)=(5列)⊕(6列)=4a639f5b⊕36000000= 7c639f5b的形式获得第7列的值。
最后,对于
W [36] = W [40](第40行的第7列)= d014f9a8 7c639f5b = ac7766f3。
通过类推进一步计算得出最终结果-密码密钥。
有关w和RotWord,Rcon和SubWord函数的更多信息。假设我们用文档中的Kr [j]-第r个回合密钥的第j个字节和w [i]表示。
我们得到:Kr =(w [Nk∙r],w [Nk∙r + 1],···,w [Nk∙r + Nk-1])。
对于不同的i,
对于i≠0 mod Nk,Nk≤i <Nb∙(Nr +1),w [i] = w [i-Nk] xor w [i-1]和
对于i = 0 mod Nk,w [i] = w [i-Nk] xor子字(RotWord(w [i – 1]))xorRcon [i / Nk]。
因此,对于i≠0modNk,Nk0≤i<Nb∙(Nr + 1)–Nk,w [i] = w [i + Nk] xor w [i + Nk-1],而对于i = 0modNk,w [i] = w [i + Nk] xorSubWord(RotWord(w [i + Nk – 1]))xorRcon [i + Nk / Nk]
对于AES-256,当i相当于4mod Nk时,您需要添加子字操作。因此,可以从最终子密钥中推断出先前的密钥,并逐步获得密码密钥的值K0。
AES-128密码的数学基础在这里非常完整和详细。
让我们转到字段映射ℓ:GF(2 8)→GF(2 8); x→x 2 + x。这个地图的图像
1= IM(升)具有尺寸暗淡GF(2)(1)= 7。
方程x2 + x =θ,其中θ1有两个不同的解(方程式的根)1,2єGF(2 8)。
根据维埃塔定理,x1⊕x2= 1,根的总和等于x 2处具有相反符号的方程的系数,根x1⊗x2=θ的乘积等于方程的自由项(在我们的方程中具有相反符号)。
众所周知,在二进制字段的算术中,元素mod2的加减运算是等效的。

因此,方程的根与比率x2 =x1⊕1相关,因为方程中x处的系数为1。这意味着在按字典顺序排列的字段元素的小数表示中,它们一个接一个地定位,仅相差一个。
因此,对于x = 0和x = 1,对于x = 2和x = 3,我们得到:

缩小对(0,1)中的映射结果(图像);(2,3)完全重合,即 两种类型对应于一张图像。因此,图像的基数比原图像的基数小两倍,并且其元素的维数为7。
成对的根的乘积(即二次方程的自由项)可以通过场元素的幂表示方便地确定(逆像)。在这种情况下,将指数加总为mod255,即 对字段GF(2 8)的乘法组的阶取模。