这是有关堆排序的系列文章中的最后一篇。在以前的讲座中，我们研究了各种各样的堆结构，这些堆结构显示了出色的速度结果。这就引出了一个问题：排序时哪个堆最有效？答案是：我们今天要看的那个。
我们前面看过的奇特堆很好，但是最有效的堆是具有改进清除功能的标准堆。
EDISON .
— « » — -, CRM-, , iOS Android.
;-)
清除是什么，为什么需要在堆中使用它，以及它如何工作，请参见系列文章的第一部分。
经典堆排序中的标准筛选大致是“正面”的-子树的根元素发送到剪贴板，分支的元素根据比较结果上移。一切都非常简单，但是事实证明，比较太多了。
在上升屏幕中，由于父母几乎不与后代进行比较，因此保存比较，基本上，仅将后代进行比较。在正常的堆排序中，将父对象与后代进行比较，并将后代彼此进行比较-因此，在交换次数相同的情况下，比较几乎是原来的一倍半。
因此，如何工作，让我们看一个具体的例子。假设我们有一个数组，其中几乎已经形成了一个堆-剩下的只是筛选根。对于所有其他节点，该条件均得到满足-任何子项均不大于其父项。
首先，从要执行清除的节点上，您需要沿着大后代前进。堆是二进制的-也就是说，我们有一个左孩子和一个右孩子。我们转到后代较大的分支。在此阶段，比较的主要次数发生了-左/右子对象相互比较。
在到达最后一级的工作表后，我们由此决定了需要上移值的分支。但是，您不需要移动整个分支，而只需移动比开始时的根更大的部分即可。
因此，我们向上分支到最近的节点，该节点大于根。
最后一步是使用缓冲区变量将节点值向上移动到分支。
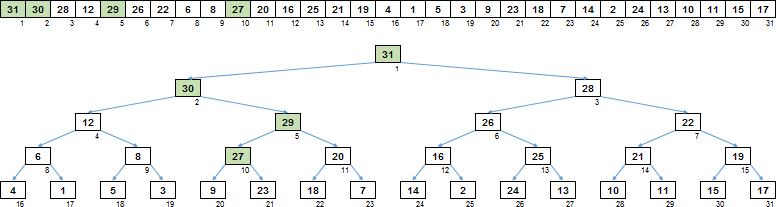
而已。升序清除已从数组形成排序树，其中任何父项都大于其后代。
最终动画：
Python 3.7实施
基本排序算法与通常的堆排序没有区别：
#
def HeapSortBottomUp(data):
#
# -
# ( )
for start in range((len(data) - 2) // 2, -1, -1):
HeapSortBottomUp_Sift(data, start, len(data) - 1)
#
# .
for end in range(len(data) - 1, 0, -1):
#
#
data[end], data[0] = data[0], data[end]
#
#
#
HeapSortBottomUp_Sift(data, 0, end - 1)
return data可以通过单独的功能方便地/直观地看到底部的下降：
#
#
def HeapSortBottomUp_LeafSearch(data, start, end):
current = start
# ,
# ( )
while True:
child = current * 2 + 1 #
# ,
if child + 1 > end:
break
# ,
if data[child + 1] > data[child]:
current = child + 1
else:
current = child
# ,
child = current * 2 + 1 #
if child <= end:
current = child
return current最重要的是-清理，首先下降，然后上升：
#
def HeapSortBottomUp_Sift(data, start, end):
#
current = HeapSortBottomUp_LeafSearch(data, start, end)
# ,
#
while data[start] > data[current]:
current = (current - 1) // 2
# ,
#
temp = data[current]
data[current] = data[start]
#
# -
while current > start:
current = (current - 1) // 2
temp, data[current] = data[current], temp
在互联网上，也找到了C语言中的代码
/*----------------------------------------------------------------------*/
/* BOTTOM-UP HEAPSORT */
/* Written by J. Teuhola <teuhola@cs.utu.fi>; the original idea is */
/* probably due to R.W. Floyd. Thereafter it has been used by many */
/* authors, among others S. Carlsson and I. Wegener. Building the heap */
/* bottom-up is also due to R. W. Floyd: Treesort 3 (Algorithm 245), */
/* Communications of the ACM 7, p. 701, 1964. */
/*----------------------------------------------------------------------*/
#define element float
/*-----------------------------------------------------------------------*/
/* The sift-up procedure sinks a hole from v[i] to leaf and then sifts */
/* the original v[i] element from the leaf level up. This is the main */
/* idea of bottom-up heapsort. */
/*-----------------------------------------------------------------------*/
static void siftup(v, i, n) element v[]; int i, n; {
int j, start;
element x;
start = i;
x = v[i];
j = i << 1;
/* Leaf Search */
while(j <= n) {
if(j < n) if v[j] < v[j + 1]) j++;
v[i] = v[j];
i = j;
j = i << 1;
}
/* Siftup */
j = i >> 1;
while(j >= start) {
if(v[j] < x) {
v[i] = v[j];
i = j;
j = i >> 1;
} else break;
}
v[i] = x;
} /* End of siftup */
/*----------------------------------------------------------------------*/
/* The heapsort procedure; the original array is r[0..n-1], but here */
/* it is shifted to vector v[1..n], for convenience. */
/*----------------------------------------------------------------------*/
void bottom_up_heapsort(r, n) element r[]; int n; {
int k;
element x;
element *v;
v = r - 1; /* The address shift */
/* Build the heap bottom-up, using siftup. */
for (k = n >> 1; k > 1; k--) siftup(v, k, n);
/* The main loop of sorting follows. The root is swapped with the last */
/* leaf after each sift-up. */
for(k = n; k > 1; k--) {
siftup(v, 1, k);
x = v[k];
v[k] = v[1];
v[1] = x;
}
} /* End of bottom_up_heapsort */纯粹凭经验-根据我的测量，升序堆排序比常规堆排序快1.5倍。
根据一些信息（在Wikipedia中的算法页面上，在“链接”部分中引用的PDF中），BottomUp HeapSort平均而言甚至比快速排序还要先进-对于16,000个或更多元素的相当大的数组。
参考资料
自下而上的堆
排序几乎具有最佳比较数量的
堆排序变体快速构建堆平均而言，堆
排序的新变种击败了快速排序（如果n不是非常小）
系列文章：
今天的排序已添加到正在使用它的AlgoLab应用程序中-使用宏更新excel文件。