记住Dijkstra的算法
Dijkstra的算法是最流行的图论算法之一。它用于查找有向图上节点之间的最短路径。我们从源节点和节点之间的已知边长开始。
首先,我们将从源到所有节点的距离值分配。节点s的值为0,因为它是源。其余的以∞值开始。
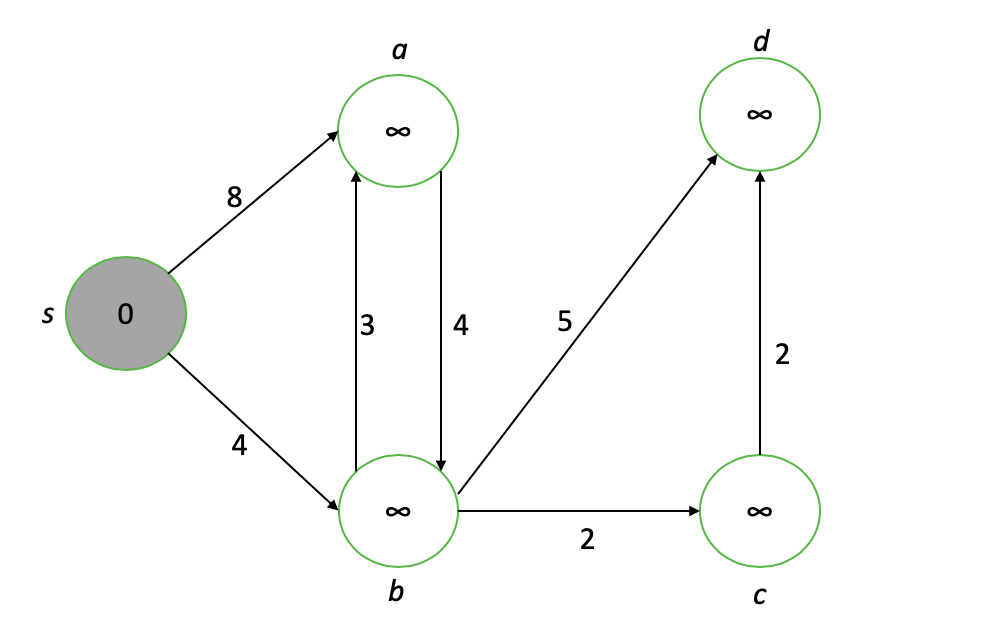
我们感兴趣的节点是具有最低值(以灰色显示)s的原始节点。首先,我们将每个相邻顶点``削弱''到我们感兴趣的节点,将其值更新为当前值或感兴趣节点的值加上连接边的长度的最小值...
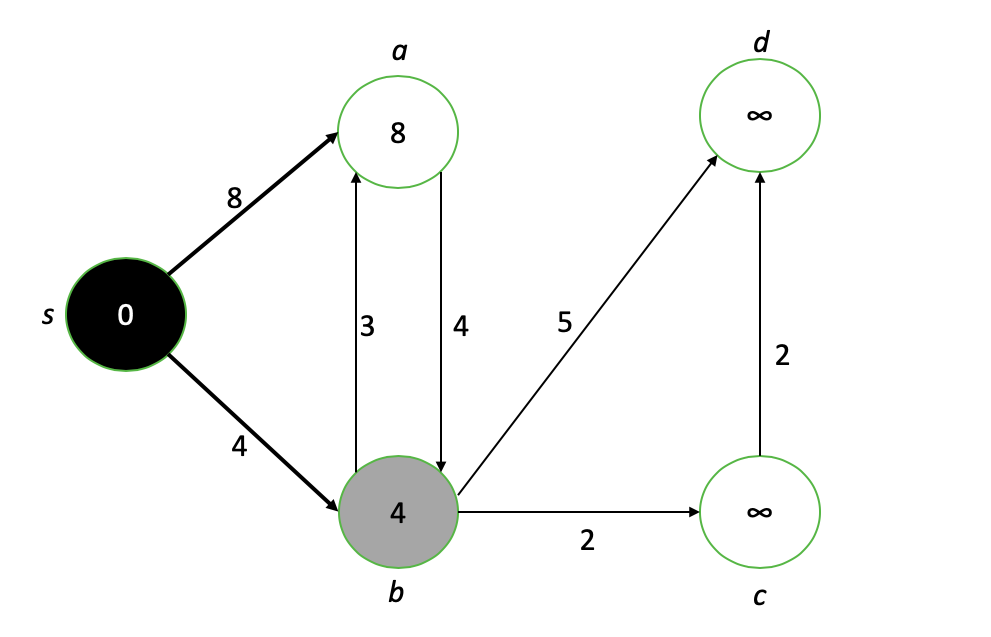
节点s现在完成(黑色),并且其邻居a和b具有其新值。感兴趣的新节点是b,因此我们重复“弱化” b的邻居并最终确定b的最短路径值的过程。

经过每个节点之后,我们最终将获得一个图表,显示从源到每个节点的最短路径长度。
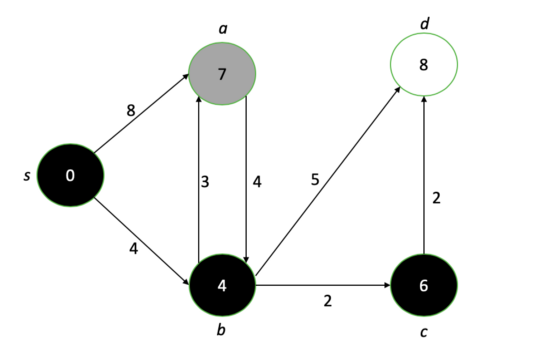


运行Dijkstra算法后的最终图表。每个节点上的数字表示距源节点的最短距离。
概念化迷宫图像

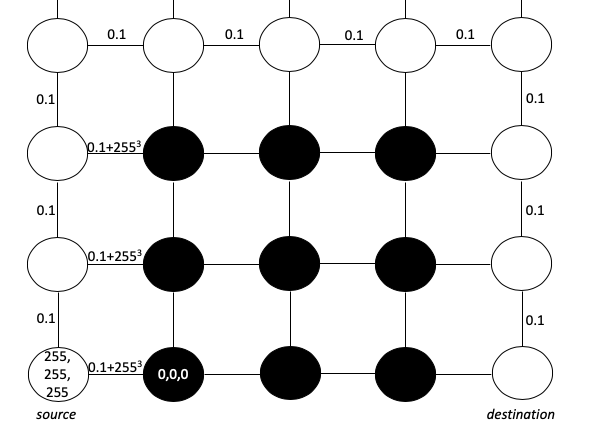
我们可以将图像想象为像素矩阵。每个像素(为简单起见)的值为RGB 0,0,0(黑色)或255,255,255(白色)。我们的目标是创建一条最短的路径,该路径从白色开始,并且不会越过黑色边界。为了表示该目标,我们可以将每个像素视为一个节点,并根据RGB值的差异绘制边缘长度在相邻像素之间的边缘。我们将使用欧几里德平方距离公式,并添加0.1以确保没有路径长度0-(对Dijkstra算法的要求):
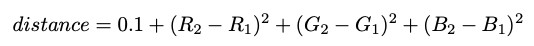
该公式使迷宫边界上的相交距离过大。如我们所见,从源头到目的地的最短路径显然将绕过障碍物,而不是通过障碍物。
实作
我们可以使用OpenCV(一个流行的Python计算机视觉库)提取像素值并显示迷宫图像。我们还通过在迷宫中添加点来定义起点和终点的坐标
import cv2
import matplotlib.pyplot as plt
import numpy as np
img = cv2.imread('maze.png') # read an image from a file using
cv2.circle(img,(5,220), 3, (255,0,0), -1) # add a circle at (5, 220)
cv2.circle(img, (25,5), 3, (0,0,255), -1) # add a circle at (5,5)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image
plt.show()
我们正在创建一个Vertex类,它将帮助我们跟踪坐标。我们还希望跟踪父节点,以便一旦找到距离值就可以重建整个路径。
class Vertex:
def __init__(self,x_coord,y_coord):
self.x=x_coord
self.y=y_coord
self.d=float('inf') #current distance from source node
self.parent_x=None
self.parent_y=None
self.processed=False
self.index_in_queue=None我们需要创建一个表示图像中像素的二维排列的顶点矩阵。这将是Dijkstra算法的基础。我们还维护一个低优先级队列,以跟踪未处理的节点。
def find_shortest_path(img,src,dst):
pq=[] #min-heap priority queue
imagerows,imagecols=img.shape[0],img.shape[1]
matrix = np.full((imagerows, imagecols), None)
#access matrix elements by matrix[row][col]
#fill matrix with vertices
for r in range(imagerows):
for c in range(imagecols):
matrix[r][c]=Vertex(c,r)
matrix[r][c].index_in_queue=len(pq)
pq.append(matrix[r][c])
#set source distance value to 0
matrix[source_y][source_x].d=0
#maintain min-heap invariant (minimum d Vertex at list index 0)
pq = bubble_up(pq, matrix[source_y][source_x].index_in_queue)我们需要一些辅助函数来帮助我们找到顶点之间的边以及边的长度:
#Implement euclidean squared distance formula
def get_distance(img,u,v):
return 0.1 + (float(img[v][0])-float(img[u][0]))**2+(float(img[v][1])-float(img[u][1]))**2+(float(img[v][2])-float(img[u][2]))**2
#Return neighbor directly above, below, right, and left
def get_neighbors(mat,r,c):
shape=mat.shape
neighbors=[]
#ensure neighbors are within image boundaries
if r > 0 and not mat[r-1][c].processed:
neighbors.append(mat[r-1][c])
if r < shape[0] - 1 and not mat[r+1][c].processed:
neighbors.append(mat[r+1][c])
if c > 0 and not mat[r][c-1].processed:
neighbors.append(mat[r][c-1])
if c < shape[1] - 1 and not mat[r][c+1].processed:
neighbors.append(mat[r][c+1])
return neighbors现在我们可以实现Dijkstra的算法并将距离值(d)分配给迷宫图像中所有像素的顶点:
while len(pq) > 0:
u=pq[0] #smallest-value unprocessed node
#remove node of interest from the queue
pq[0]=pq[-1]
pq[0].index_in_queue=0
pq.pop()
pq=bubble_down(pq,0) #min-heap function, see source code
u.processed=True
neighbors = get_neighbors(matrix,u.y,u.x)
for v in neighbors:
dist=get_distance(img,(u.y,u.x),(v.y,v.x))
if u.d + dist < v.d:
v.d = u.d+dist
v.parent_x=u.x #keep track of the shortest path
v.parent_y=u.y
idx=v.index_in_queue
pq=bubble_down(pq,idx)
pq=bubble_up(pq,idx)现在我们可以调用最短路径函数并在迷宫中绘制解决方案:
img = cv2.imread('maze.png') # read an image from a file using opencv (cv2) library
p = find_shortest_path(img, (25,5), (5,220))
drawPath(img,p)
plt.figure(figsize=(7,7))
plt.imshow(img) # show the image on the screen
plt.show()

让我们尝试来自Internet的其他迷宫。

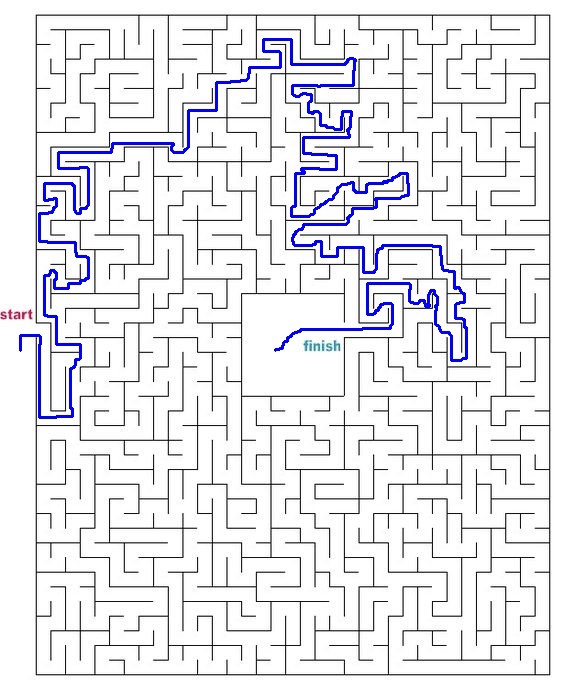


完整的源代码可以在GitHub上找到。
继续:一个Python培训项目:带有40行代码的界面(第2部分)

了解更多有关如何通过接受SkillFactory付费在线课程来从零开始或获得技能和薪资水平晋升的方法:
- 机器学习课程(12周)
- 从头开始培训数据科学专业(12个月)
- 具备任何入门水平的分析专业(9个月)
- «Python -» (9 )