FAISS：快速搜索数百万美元数据中的面孔和克隆

有一次，在DAN小组每年举行一次客户会议的前夕，我们思考可以考虑一些有趣的事情，以便我们的合作伙伴和客户对活动有愉快的印象和记忆。我们决定分析这次会议中成千上万张照片的存档和几张过去的照片（当时有18张）：一个人向我们发送了他的照片，然后在几秒钟内我们从他的存档中向他发送了一些精选的照片，为期数年。



我们没有发明自行车，而是使用了著名的dlib库并接收了每个人的嵌入（矢量表示）。 



为了方便起见，我们添加了一个Telegram机器人，一切都很好。从人脸识别算法的角度来看，一切都奏效，但会议结束了，我不想放弃使用久经考验的技术。我想从几千人发展到数亿，但我们没有特定的业务任务。一段时间后，我们的同事完成了一项任务，需要处理如此大量的数据。



问题是要在Instagram上编写一个智能机器人监控系统。在这里，我们的想法导致了一种简单而复杂的方法：



简单的方式：我们考虑所有订阅比订阅者多，没有头像，没有填写全名的帐户，等等。结果，我们得到了半死不清的账目。



艰难的方法：由于现代机器人已经变得越来越聪明，现在他们发布帖子，睡觉甚至编写内容，所以出现了一个问题：如何捕捉这些东西？首先，密切监视他们的朋友，因为他们经常也是机器人，并跟踪重复的照片。其次，很少有机器人知道如何生成自己的图片（尽管这是可能的）），这意味着在Instagram上使用不同帐户复制人的照片是找到机器人网络的良好触发。

下一步是什么？

如果简单的方法可以很好地预测并且很快就能得到结果，那么困难的方法就很难实现，因为要实现该方法，我们将必须矢量化并建立索引，以进行相似的比较，以处理数量惊人的大量照片-数百万甚至数十亿张照片。如何付诸实践？毕竟，出现技术问题：

1. 搜索速度和准确性
2. 数据占用的磁盘空间
3. 已使用的RAM存储器的大小。 

如果只有几张照片，至少不超过一万张照片，我们可以将自己局限于矢量聚类的简单解决方案，但是要处理大量矢量，并找到某个矢量的最近邻居，则需要复杂且优化的算法。



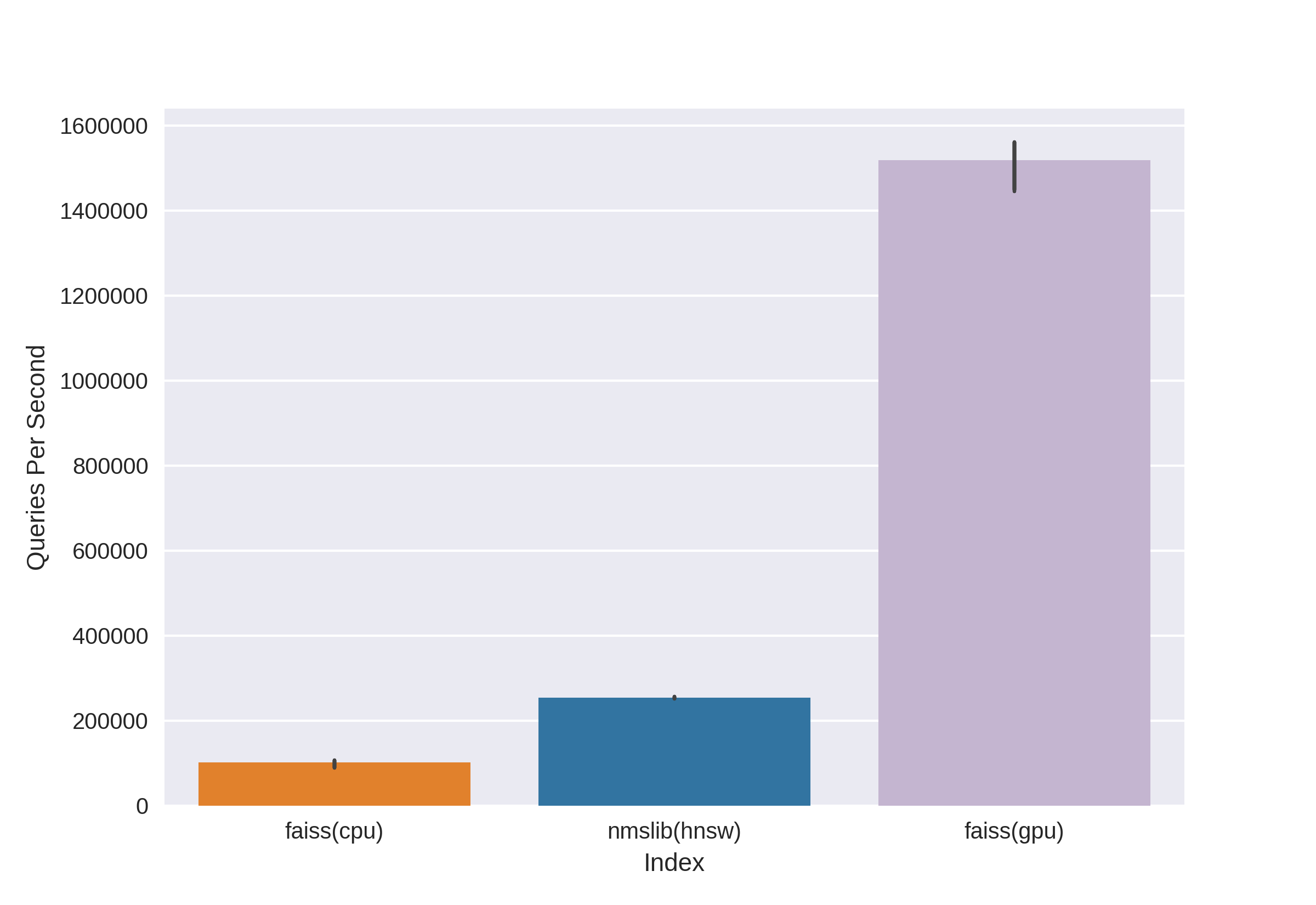
有众所周知的成熟技术，例如Annoy，FAISS，HNSW。nmslib和hnswlib库中提供的快速HNSW邻居搜索算法，显示了CPU上的最新结果，可以从相同的基准测试中看到。但是我们会立即将其切断，因为我们对处理大量数据时使用的内存量不满意。我们开始在Annoy和FAISS之间进行选择，最后选择FAISS是因为它具有便利性，较少的内存使用量，GPU的潜在使用量以及性能基准（例如，您可以在此处看到）。顺便说一句，在FAISS中，HNSW算法被实现为一种选择。

什么是FAISS？

Facebook AI Research相似性搜索 -由Facebook AI Research团队开发，可快速查找最近的邻居并在矢量空间中聚类。高搜索速度允许处理非常大的数据-多达数十亿个向量。



FAISS的主要优点是其在GPU上的最新结果，而在CPU上的实现则稍逊于hnsw（nmslib）。我们希望能够同时在CPU和GPU上进行搜索。此外，FAISS在内存使用和大批量搜索方面进行了优化。



Source



FAISS可让您快速搜索给定向量x的k个最近向量。但是，这种搜索是如何进行的呢？

指标

FAISS的主要概念是index，实质上，它只是参数和向量的集合。参数集完全不同，取决于用户的需求。向量可以保持不变，也可以重新排列。将向量添加到其中后，有些索引可立即使用，而有些则需要事先培训。向量名称存储在索引中：以从0到n的编号或适合Int64类型的数字存储。



第一个索引（也是我们在会议上使用的最简单的索引）是Flat。它仅存储所有向量本身，并且通过穷举搜索执行对给定向量的搜索，因此无需对其进行训练（但下面的训练更多）。对于少量数据，这种简单的索引很可能满足您的搜索需求。



例：

import numpy as np
dim = 512  #     512
nb = 10000  #    
nq = 5 #      
np.random.seed(228)
vectors = np.random.random((nb, dim)).astype('float32')
query = np.random.random((nq, dim)).astype('float32')

创建平面索引并无需训练即可添加向量：

import faiss
index = faiss.IndexFlatL2(dim)
print(index.ntotal)  #   
index.add(vectors)
print(index.ntotal)  #    10 000 

现在让我们从向量中找到前五个向量的7个最近邻居：

topn = 7
D, I = index.search(vectors[:5], topn)  #  : Distances, Indices
print(I)
print(D)

我们看到距离为0的最接近的邻居是向量本身，其余的则通过增加距离来确定范围。让我们从查询中搜索向量：

D, I = index.search(query, topn) 
print(I)
print(D)

现在，结果第一列中的距离不为零，因为来自查询的向量不在索引中。



索引可以保存到磁盘，然后从磁盘加载：

faiss.write_index(index, "flat.index")
index = faiss.read_index("flat.index")

看来一切都是基本的！几行代码-我们已经有了搜索高维向量的结构。但是，只有一千万个512维矢量的索引将重约20GB，并且在使用时占用相同数量的RAM。



在会议项目中，我们只使用了具有统一索引的基本方法，由于数据量相对较少，一切都很棒，但是现在我们正在谈论数以亿计的高维向量！

通过倒排列表加快搜索速度

源



FAISS的最主要和最酷的功能是IVF索引，即“反向文件”索引。倒转文件的想法是简单的，用手指可以很好地解释：



让我们想象一下一支庞大的军队，由最多的杂色战士组成，例如有100万人。马上指挥整个部队是不可能的。按照军事惯例，我们需要将部队分为多个子单位。让我们分为$$$\sqrt{1 000 000} = 1000$大约相等的部分，从每个单位中选择一名代表作为指挥官。我们将尝试发送尽可能相似的字符，来源，物理数据等。战士在一个单位中，我们将选择指挥官，以便他尽可能准确地代表他的单位-他是“平均”的人。结果，我们的任务从指挥一百万士兵减少到通过指挥官指挥1000个单位，由于我们知道指挥官是什么，我们对我军的组成有很好的想法。



这就是IVF索引的思想：让我们使用k-means算法将一大组矢量逐个分组与每个部分相对应的质心是一个向量，它是给定簇的选定中心。我们将搜索到质心的最小距离，然后才在与该质心相对应的聚类中寻找向量之间的最小距离。取k等于$$$\sqrt{n}$哪里 $$$n$ -索引中向量的数量，我们将在两个级别上获得最佳搜索-首先是 $$$\sqrt{n}$ 重心，然后 $$$\sqrt{n}$每个簇中的向量。搜索比蛮力搜索快得多，后者解决了使用数百万个向量时的问题之一。





向量空间通过k-means方法划分为k个簇。每个群集都分配了一个质心



示例代码：

dim = 512
k = 1000  #  “”
quantiser = faiss.IndexFlatL2(dim) 
index = faiss.IndexIVFFlat(quantiser, dim, k)
vectors = np.random.random((1000000, dim)).astype('float32')  # 1 000 000 “”

您可以使用方便的FAISS东西建立索引，从而更加优雅地编写它：

index = faiss.index_factory(dim, “IVF1000,Flat”)
 :
print(index.is_trained)   # False.
index.train(vectors)  # Train    
 
#  ,      ,      :
print(index.is_trained)  # True
print(index.ntotal)   # 0
index.add(vectors)
print(index.ntotal)   # 1000000

在Flat之后检查了这种类型的索引，我们解决了我们潜在的问题之一-搜索速度，它比穷举搜索要低几倍。

D, I = index.search(query, topn) 
print(I)
print(D)

但是有一个“但是”-搜索的准确性以及速度将取决于访问的簇的数量，可以使用nprobe参数进行设置：

print(index.nprobe)  # 1 –           
index.nprobe = 16  #   -16    top-n  
D, I = index.search(query, topn) 
print(I)
print(D)

如您所见，增加nprobe后，我们得到了完全不同的结果，D中最小距离的顶部变好了。



您可以使nprobe等于索引中的质心数，这相当于通过穷举搜索进行搜索，精度最高，但搜索速度会明显下降。

搜索磁盘-在磁盘反向列表上

好了，我们解决了第一个问题，现在在数以千万计的向量上，我们获得了可接受的搜索速度！但是，只要我们的巨大索引不适合RAM，所有这些都是无用的。



专门针对我们的任务，FAISS的主要优点是能够将Inverted Lists IVF索引存储在磁盘上，仅将元数据加载到RAM中。



我们如何创建这样的索引：我们使用必要的参数对indexIVF进行训练，以适应内存中最大可能的数据量，然后将向量（不仅经过训练的人）添加到零件中经过训练的索引中，并将每个零件的索引写入磁盘。

index = faiss.index_factory(512, “,IVF65536, Flat”, faiss.METRIC_L2)

我们以这种方式在GPU上训练索引：

res = faiss.StandardGpuResources()
index_ivf = faiss.extract_index_ivf(index)
index_flat = faiss.IndexFlatL2(512)
clustering_index = faiss.index_cpu_to_gpu(res, 0, index_flat)  #  0 –  GPU
index_ivf.clustering_index = clustering_index

faiss.index_cpu_to_gpu（res，0，index_flat）可以替换为faiss.index_cpu_to_all_gpus（index_flat）以一起使用所有GPU。



非常需要训练样本尽可能具有代表性并具有均匀的分布，因此我们从所需数量的向量中预先组成训练数据集，并从整个数据集中随机选择它们。

train_vectors = ...  #     
index.train(train_vectors)

#    ,   :
faiss.write_index(index, "trained_block.index") 

#       
#      :
for bno in range(first_block, last_block+ 1):
    block_vectors = vectors_parts[bno]
    block_vectors_ids = vectors_parts_ids[bno]  # id ,  
    index = faiss.read_index("trained_block.index")
    index.add_with_ids(block_vectors, block_vectors_ids)
    faiss.write_index(index, "block_{}.index".format(bno))

之后，我们将所有反向列表合并在一起。这是可能的，因为实际上每个块都是相同的训练索引，只是内部带有不同的向量。

ivfs = []
for bno in range(first_block, last_block+ 1):
    index = faiss.read_index("block_{}.index".format(bno), faiss.IO_FLAG_MMAP)
    ivfs.append(index.invlists)
    #  index   inv_lists 
    #        :
    index.own_invlists = False

#   :
index = faiss.read_index("trained_block.index")

#   invlists
#  invlists       merged_index.ivfdata
invlists = faiss.OnDiskInvertedLists(index.nlist, index.code_size, "merged_index.ivfdata")
ivf_vector = faiss.InvertedListsPtrVector() 

for ivf in ivfs: 
    ivf_vector.push_back(ivf)

ntotal = invlists.merge_from(ivf_vector.data(), ivf_vector.size())
index.ntotal = ntotal  #     
index.replace_invlists(invlists)  
faiss.write_index(index, data_path + "populated.index")  #    

底线：现在，我们的索引是populated.index和merged_blocks.ivfdata文件。



在populated.index中，使用反向列表记录了文件的原始完整路径，因此，如果文件路径ivfdata由于某种原因而更改了索引的读取，则需要使用标志faiss.IO_FLAG_ONDISK_SAME_DIR，该标志使您可以在与目录相同的目录中搜索ivfdata文件。填充索引：

index = faiss.read_index('populated.index', faiss.IO_FLAG_ONDISK_SAME_DIR)

GiISS的FAISS项目演示示例 作为基础。



可以在FAISS Wiki上查看迷你索引索引指南。例如，我们能够将一个1200万个向量的训练数据集拟合到RAM中，因此我们在262144个质心上选择了IVFFlat索引，然后扩展到数亿个。该指南还建议使用IVF262144_HNSW32索引，在该索引中，属于簇的向量是由具有32个最近邻居的HNSW算法确定的（换句话说，使用了量化器IndexHNSWFlat），但是，正如我们在进一步测试中所看到的那样，对这种索引的搜索不太准确。另外，应该记住，这种量化器排除了在GPU上使用的可能性。

通过产品量化显着减少磁盘使用

由于使用了磁盘搜索方法，因此可以消除RAM中的负载，但是具有一百万个向量的索引仍然占用了大约2 GB的磁盘空间，而我们正在谈论使用数十亿个向量的可能性，这将需要两个以上的TB！当然，如果您设定目标并分配额外的磁盘空间，容量不会那么大，但是这让我们有些烦恼。



向量的编码即标量量化（SQ）和乘积量化（PQ）。 SQ-将向量的每个分量编码为n位（通常为8、6或4位）。我们将考虑PQ选项，因为用8位编码一个float32组件的想法在精度损失方面看起来太令人沮丧。尽管在某些情况下，将SQfp16压缩为float16几乎不会造成任何损失。



乘积量化的本质如下：维数为512的矢量被分为n个部分，每个部分被分为256个可能的簇（1个字节），即 我们用n个字节表示向量，其中FAISS实现中n通常不超过64。但是，这种量化不应用于数据集中的向量本身，而是应用于这些向量与在生成“反向列表”阶段获得的相应质心的差异！事实证明，反向列表将被编码为向量及其质心之间的距离集。

index = faiss.index_factory(dim, "IVF262144,PQ64", faiss.METRIC_L2)

事实证明，现在我们不需要存储所有向量-足以为每个向量分配n个字节，为每个质心向量分配2048个字节。就我们而言，$$$n = 64$，即 $$$\frac{512}{64} = 8$-一个子向量的长度，在256个簇之一中定义。







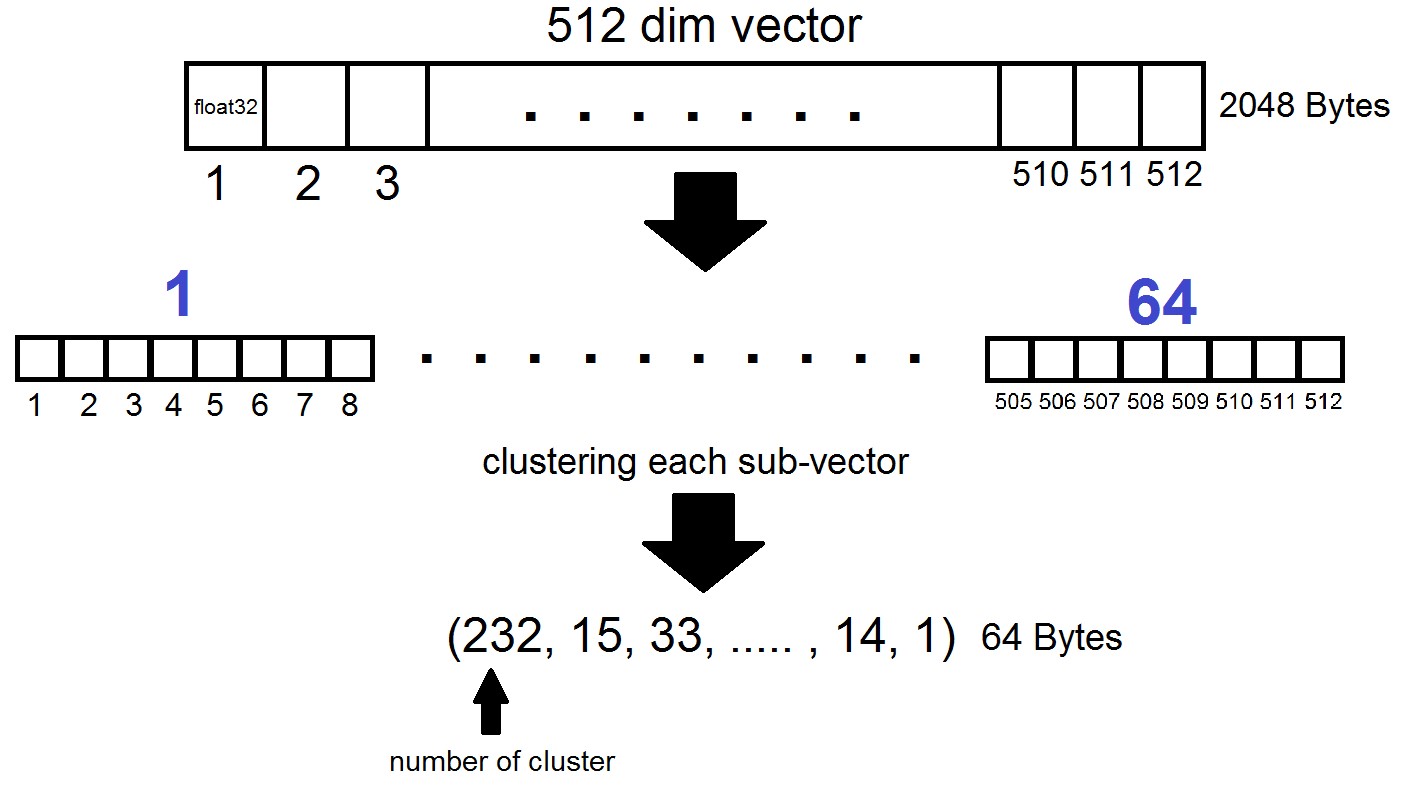
当按向量x搜索时，最接近的质心将首先使用常规的Flat量化器确定，然后x也被划分为子矢量，每个子矢量都由256个相应质心之一的数量编码。到向量的距离定义为子向量之间64个距离的总和。

底线是什么？

我们停止了对“ IVF262144，PQ64”索引的实验，因为它完全满足了我们对搜索速度和准确性的所有需求，并且在进一步扩展索引的同时确保了磁盘空间的合理使用。更具体地说，目前，该索引具有3.15亿个向量，占用22 GB磁盘空间和约3 GB RAM。



我们之前没有提到的另一个有趣的细节是索引使用的度量。默认情况下，以欧几里得L2度量标准来计算任意两个向量之间的距离，或者以更易理解的语言来计算，该距离被作为坐标方向差的平方和的平方根来计算。但是您可以设置另一个指标，尤其是我们测试了METRIC_INNER_PRODUCT指标，或向量之间的余弦距离的度量。之所以是余弦的，是因为欧几里得坐标系中两个向量之间的角度的余弦表示为向量的标量（坐标）乘积与其长度的乘积之比，并且如果空间中所有向量的长度均为1，则角度的余弦将完全等于坐标的乘积。在这种情况下，向量在空间中的距离越近，其点积就越接近一个。



度量L2具有到标量乘积度量的直接数学转换。但是，通过实验比较这两个指标时，印象是标量产品的指标有助于我们以更成功的方式分析图像的相似系数。此外，我们的照片嵌入是使用InsightFace，它使用余弦距离实现ArcFace架构。FAISS索引中还有其他指标，您可以在此处阅读。

结论和好奇的例子

因此，回到一切开始的地方。回想起来，它的动机是解决在Instagram网络上查找机器人的问题，更具体地说，是寻找与某些用户集中的人物或头像重复的帖子。在编写材料的过程中，很明显，我们的漫游器搜索方法的详细描述是引用到另一篇文章中的，我们将在以后的出版物中进行讨论，但现在，我们将仅限于使用FAISS进行实验的示例。



您可以用不同的方式对图片或面部进行矢量化处理，我们选择了InsightFace技术（对图像进行矢量化处理并从其中提取n维特征是一个单独的故事）。在我们接受的基础设施的实验过程中，发现了相当有趣和有趣的属性。



例如，在获得同事和熟人许可的情况下，我们将他们的面孔上传到搜索中，并迅速找到了其中存在





的照片：我们的同事陷入了背景下人群中的Comic-Con访客照片。来源





野餐在一大群朋友，从朋友的帐户的照片。来源





只是路过。一位不知名的摄影师捕捉了他们的主题形象。他们不知道照片在哪里，五年之后，他们完全忘记了如何照相。来源





在这种情况下，摄影师既未知又被秘密拍摄！

立即回想起可疑的单反女孩，此刻坐在:) 来源



因此，通过简单的动作，FAISS可使您在膝盖上组装著名的FindFace的类似物。



另一个有趣的功能：在FAISS索引中，面孔彼此相似的越多，空间中的对应矢量就越接近。我决定仔细研究一下我的面部搜索结果的准确性稍差，并找到了极为相似的克隆：)





一些作者的克隆。

图片来源：1，2，  3



一般而言，FAISS开辟了一个巨大的领域中的任何创意的实现。例如，根据相似脸部向量接近的相同原理，有可能建立从一个人到另一个人的路径。或者，作为最后的手段，让FAISS成为生产此类模因的工厂：





资料来源



感谢您的关注，我们希望该材料对Habr的读者有用！



本文是在我的同事Artyom Korolev（科罗廖瓦特），帖木儿（Timur Kadyrov）和阿里娜（Arina Reshetnikova）。



研发Dentsu Aegis Network Russia。