Clever Geek Handbook

比赛排序

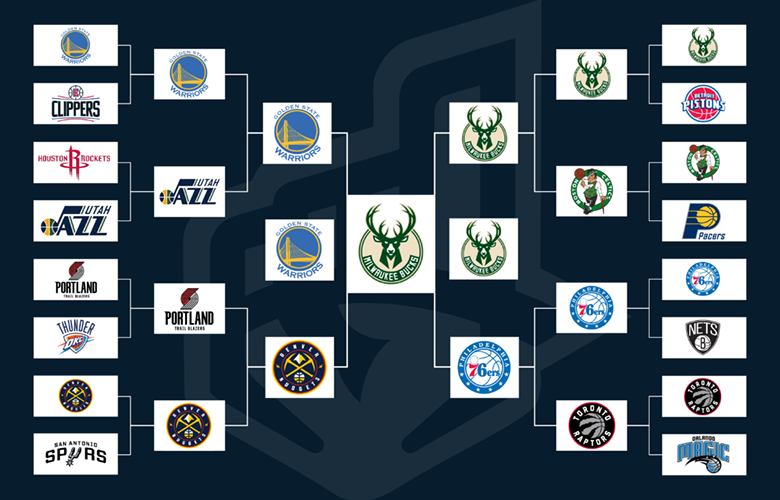
我们将继续熟悉各种堆以及使用这些堆的排序算法。今天，我们有了所谓的锦标赛树。
EDISON软件-网络开发
EDISON .




, . , .



computer science ;-)
锦标赛排序的主要思想是使用相对较小（与主数组相比）的辅助堆，该堆充当优先级队列。在此堆中，将对较低级别的元素进行比较，结果是较小的元素（在这种情况下，我们拥有MIN-HEAP的树）将上升，并且落入该堆的数组元素部分中的当前最小值将浮动到根中。最小值被转移到附加的“优胜者”数组中，结果堆将比较/移动其余元素-现在，新的最小值位于树的根中。请注意，在这样的系统中，下一个最小值比上一个最小值更大-然后可以轻松地组装一个新的“获胜者”排序数组，在​​其中将新的最小值简单地添加到附加数组的末尾。



将最小值转移到附加数组会导致以下事实：主数组下一个元素的空位出现在堆中-结果，所有元素都按照队列的顺序进行处理。



主要的微妙之处在于，除了“赢家”之外，还有“失败者”。如果某些元素已经转移到“获胜者”数组中，那么，如果未处理的元素小于这些“获胜者”数组，则在此阶段将它们筛选通过锦标赛树是没有意义的-将这些元素插入“获胜者”数组将太昂贵（在您不能结束它们，但要将它们放在开头，则必须移动先前插入的最小值。这些无法放入“获胜者”阵列的元素将被发送到“输者”阵列-当对其余输者重复所有动作时，它们将在下一个迭代之一中通过锦标赛树。



在Internet上找到该算法的实现并不容易，但是在YouTube上找到了清晰，漂​​亮的Ruby实现。“链接”部分中也提到了Java代码，但是在这里看起来不太可读。 



  #         
  require_relative "pqueue"
	
  #     
  MAX_SIZE = 16

  def tournament_sort(array)
    #   ,   ""
    return optimal_tourney_sort(array) if array.size <= MAX_SIZE
    bracketize(array) #   ,   ""
  end
	
  #     
  def bracketize(array)
	
    size = array.size
    pq = PriorityQueue.new
    #    
    pq.add(array.shift) until pq.size == MAX_SIZE
    winners = [] #  ""
    losers = [] #  ""
		
    #      
    until array.empty?
			
      #  ""  ?
      if winners.empty?
        #      ""
        winners << pq.peek
        #     
        pq.remove 
      end
			
      #      ,   ""
      if array.first > winners.last
        pq.add(array.shift) #       
      else #        ""
        losers << array.shift #     ""
      end
			
      #     ,     ""
      winners << pk.peek unless pk.peek.nil?
      pq.remove #     
			
    end
		
    #   ,      - ?
    until pq.heap.empty?
      winners << pq.peek #     ""
      pq.remove #     
    end

    #   ""  , , ,
    #  "" -   
    return winners if losers.empty?
		
    #    ,    ""
    #   ""
    array = losers + winners
    array.pop while array.size > size
    bracketize(array) #   
		
  end
	
  #       
  def optimal_tourney_sort(array)
    sorted_array = [] #    
    pq = PriorityQueue.new
    array.each { |num| pq.add(num) } #     -
    until pq.heap.empty? #  -  
      sorted_array << pq.heap[0] 
      pq.remove #     
    end
    sorted_array #  
  end
	
  # 
  if $PROGRAM_NAME == __FILE__
    #  
    shuffled_array = Array.new(30) { rand(-100 ... 100) }
    #   
    puts "Random Array: #{shuffled_array}"
    #   
    puts "Sorted Array: #{tournament_sort(shuffled_array)}"
  end


这是一个幼稚的实现，其中在将每个数组分为“失败者”和“赢家”之后，将这些数组组合在一起，然后对组合后的数组再次重复所有操作。如果在组合数组中首先有“失败”元素，则在锦标赛堆中进行筛选将与“获胜者”一起排序。





此实现非常简单直观，但是您不能称之为有效。排序后的“优胜者”会多次进入锦标赛树，这显然是多余的。我假设这里的时间复杂度是对数二次方O（n log 2 n）。



多路径合并选项



如果通过筛子的有序元素没有反复通过比赛，则算法将明显加速。



在将无序数组分为已排序的“赢家”和未排序的“失败者”之后，仅对“失败者”重新重复整个过程。在每次新的迭代中，将累积一组带有“优胜者”的数组，这种数组将继续进行，直到在某个步骤中没有“失败者”为止。之后，剩下的就是合并所有“赢家”阵列。由于所有这些数组均已排序，因此可以以最小的成本进行合并。





以这种形式，算法可能已经找到了有用的应用程序。例如，如果您必须处理大数据，则在此过程中，使用锦标赛堆将产生有序数据包，使用这些数据包，您可以在处理其他所有内容时执行某些操作。数组



的n个元素中的每个元素仅通过锦标赛树一次，这需要O（log n）时间。在这种实现中，该算法具有最差/平均时间复杂度O（n log n）。



在本季大结局



关于堆排序的系列几乎已经完成。仍有待讲述其中最有效的。



参考资料



Tournament sort



Priority queue



Tournament sort in Java



The Theory Behind the The Theory Behind the z/Architecture Sort Assist Instructions



Using Tournament Trees to Sort



Tournament Sort Demo Ruby



Tournament Sort Visualization



Tournament Sort Data Structure UGC NET DS



Tournament Sort Algorithm — a Heapsort variant



:






今天的排序已添加到使用它的AlgoLab应用程序中-使用宏更新excel文件。



在带有排序名称的单元格注释中，可以指定一些设置。

可变方式是多方锦标赛树（以防万一，可以使该树不仅是二叉树，而且还可以是三叉树，四叉树和五叉树）。队列

变量是原始队列的大小（树的最低层中的节点数）。由于树已满，例如，如果使用way = 2，则您指定queue = 5，则队列大小将增加到最接近的2的幂（在这种情况下，最大为8）。 可变NWayMerge

取值1或0-指示是否使用多路径合并。


More articles:


All Articles