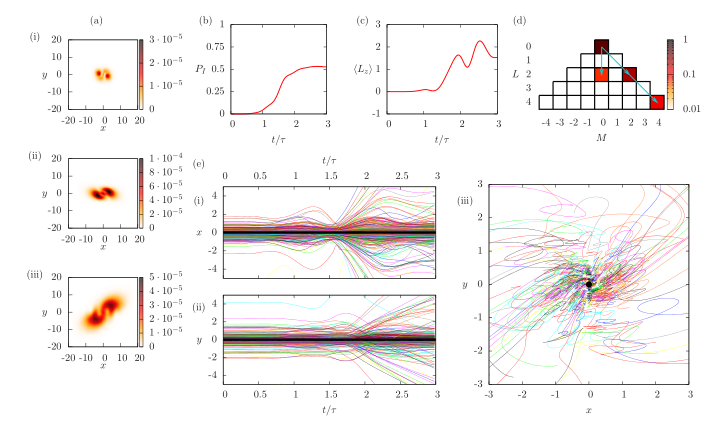
在文章的附件中,提供了粒子的路径,切出的材料:路径积分,霓虹灯冷原子的双缝实验,粒子的隐形传送框架以及其他残酷和性的场景。
我认为,除了证明数学形式主义在逻辑上是一致的之外,没有其他方法可以证明数学形式主义与经验的偏离或证明其预测不会耗尽观察的可能性。
尼尔斯·玻尔(Niels Bohr)
最后,作者想指出,我们仅接受两个理由来拒绝解释多种现象的理论。首先,该理论在内部是不一致的,其次,它与实验不一致。
大卫·鲍姆(David Bohm)
之前,我们了解了Schrödinger方程的来源,为什么从那里获取Schrödinger方程以及如何通过各种方法来获取它。
现在,让我们将其分为两个真实方程式。为此,我们以极性形式表示psi, :
S — , R — . , , , — -, ( ).
, . , S -, - - :
, -, , , , S, , , , . , , . -.
— , . , , , . , , , .
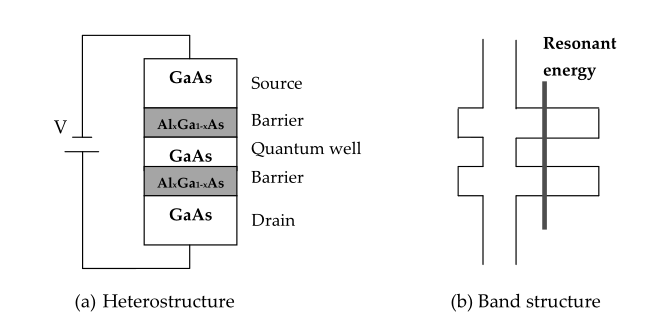
, , , . . . , , , .
, .
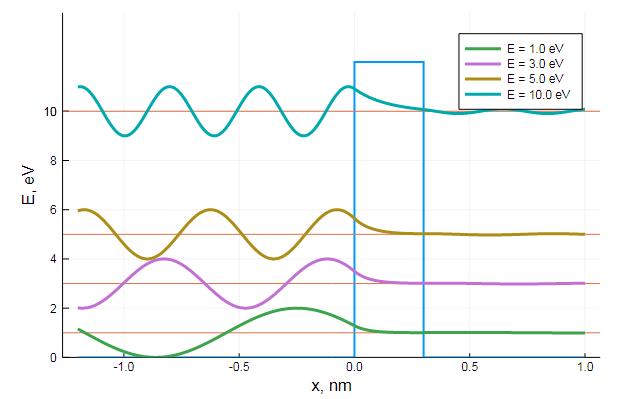
, , , . , ( - ). :
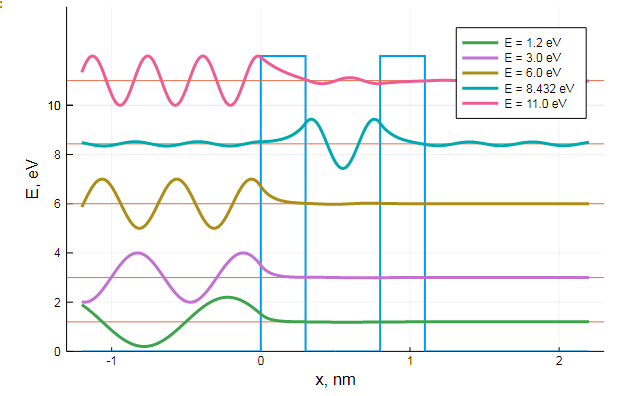
()
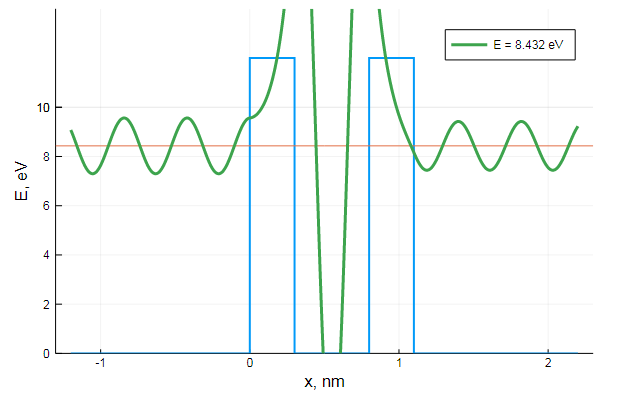
, , , : ,
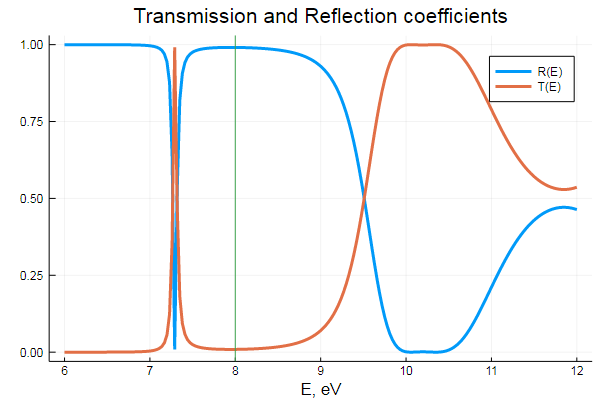
, . . .
-, :
using LinearAlgebra, SparseArrays, Plots
const ħ = 1.0546e-34 # J*s
const m = 9.1094e-31 # kg
const q = 1.6022e-19 # Kl
const nm = 1e-9 # m
const fs = 1e-12; # s
function wavefun()
gauss(x) = exp( -(x-x0)^2 / (2*σ^2) + im*x*k )
k = m*v/ħ
#
Vm = spdiagm(0 => V )
H = spdiagm(-1 => ones(Nx-1), 0 => -2ones(Nx), 1 => ones(Nx-1) )
H *= ħ^2 / ( 2m*dx^2 )
H += Vm
A = I + 0.5im*dt/ħ * H #
B = I - 0.5im*dt/ħ * H #
psi = zeros(Complex, Nx, Nt)
psi[:,1] = gauss.(x)
for t = 1:Nt-1
b = B * psi[:,t]
# A*psi = b
psi[:,t+1] = A \ b
end
return psi
enddx = 0.05nm # x step
dt = 0.01fs # t step
xlast = 400nm
Nt = 260 # Number of time steps
t = range(0, length = Nt, step = dt)
x = [0:dx:xlast;]
Nx = length(x) # Number of spatial steps
a1 = 200nm
a2 = 200.5nm # 5
a3 = 205nm
a4 = 205.5nm
#V = [ a1<xi<a2 ? 2q : 0.0 for xi in x ] # 2 eV
V = [ a1<xi<a2 || a3<xi<a4 ? 2q : 0.0 for xi in x ] # 2 eV
x0 = 80nm # Initial position
σ = 20nm # gauss width
v = -120nm/fs;
@time Psi = wavefun()
P = abs2.(Psi);
function ψ(xi, j)
k = findfirst(el-> abs(el-xi)<dx, x)
k == nothing && ( k = 1 )
Psi[k, j]
end
function corpusculaz(n)
X = zeros(n, Nt)
X[:,1] = x0 .+ σ*randn(n)
for j in 2:Nt, i in 1:n
U = ħ/(2m*dx) * imag( ( ψ(X[i,j-1]+dx, j) - ψ(X[i,j-1]-dx, j) ) / ψ(X[i,j-1], j) )
X[i,j] = X[i,j-1] - U*dt
end
X
end
@time X = corpusculaz(20);
plot(x, P[:, 1], legend = false)
plot!(x, P[:, 80], legend = false)
scatter!( X[:,1], zeros(20) )
scatter!( X[:,80], zeros(20) )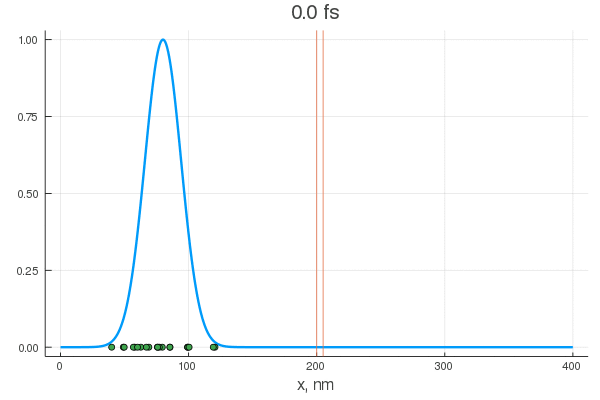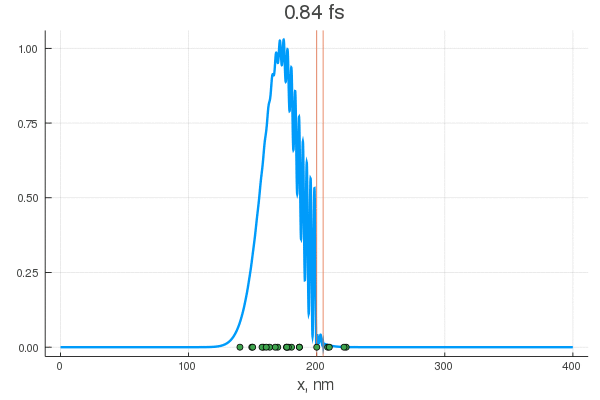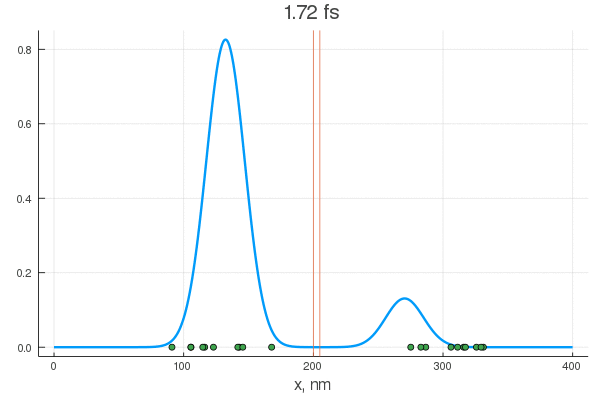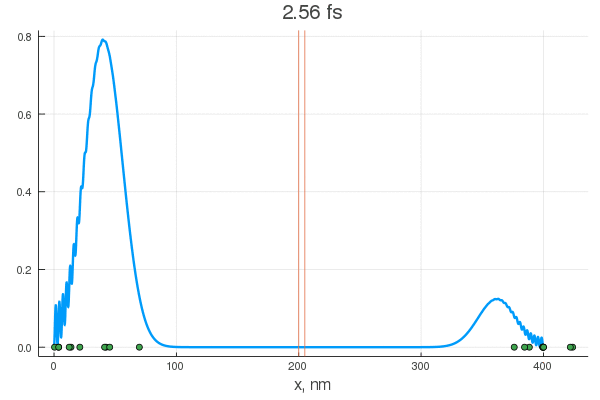
. — , . :
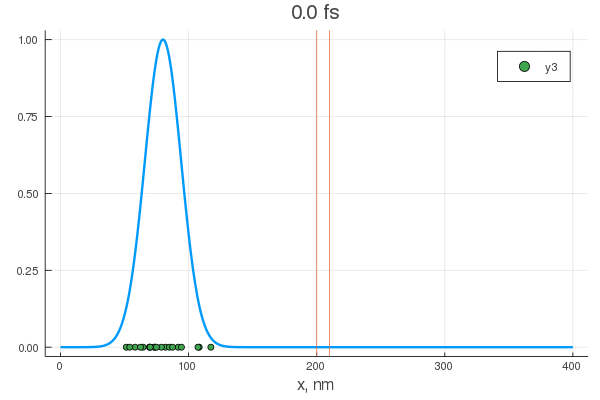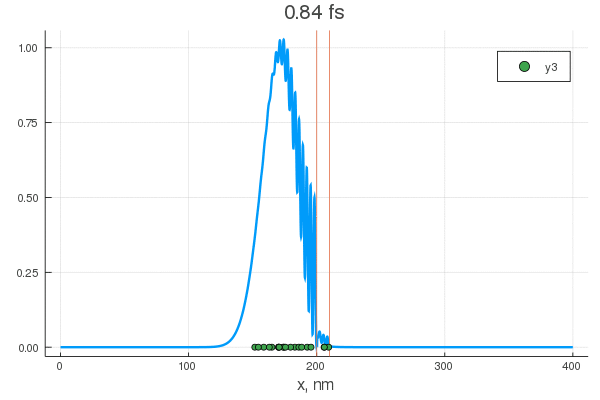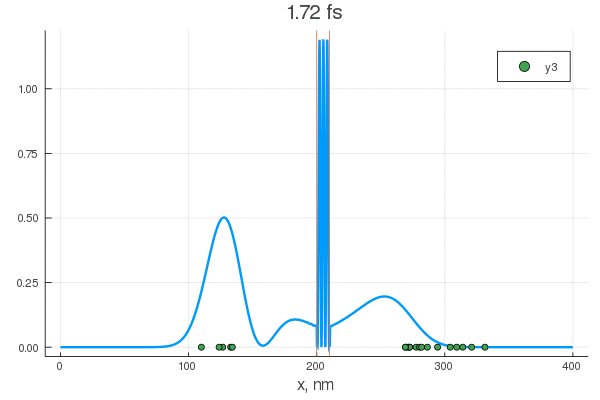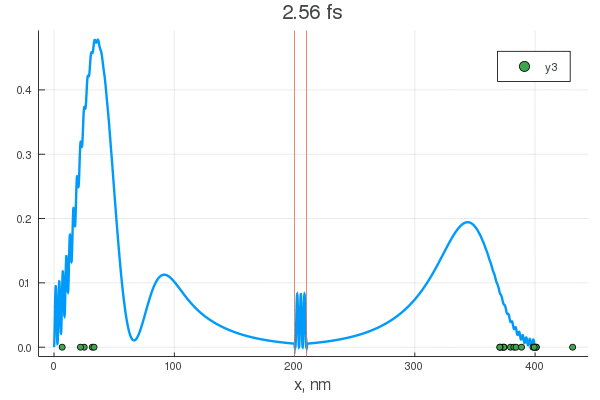
, . , , !
, . Double-slit interference with ultracold metastable neon atoms — - .
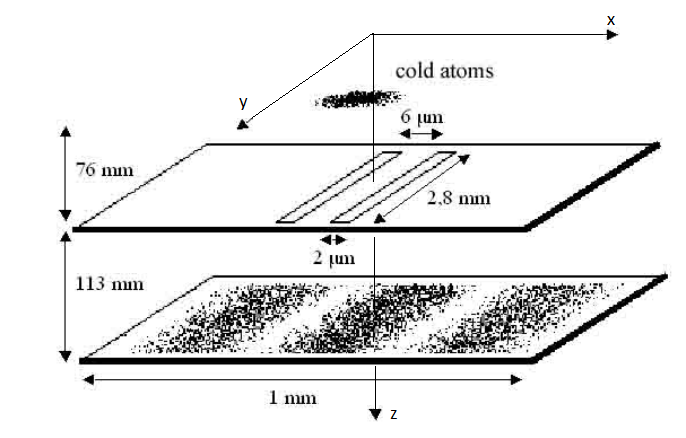
using Random, Gnuplot, Statistics
#
function trapez(f, a, b, n)
h = (b - a)/n
result = 0.5*(f(a) + f(b))
for i in 1:n-1
result += f(a + i*h)
end
result * h
end
#
function rk4(f, x, y, h)
k1 = h * f(x , y )
k2 = h * f(x + 0.5h, y + 0.5k1)
k3 = h * f(x + 0.5h, y + 0.5k2)
k4 = h * f(x + h, y + k3)
return y + (k1 + 2*(k2 + k3) + k4)/6.0
endconst ħ = 1.055e-34 # J*s
const kB = 1.381e-23 # J*K-1
const g = 9.8 # m/s^2
const l1 = 76e-3 # m
const l2 = 113e-3 # m
const yh = 2.8e-3 # m
const d = 6e-6 # m
const b = 2e-6 # m
const a1 = 0.5(- d - b) #
const a2 = 0.5(- d + b)
const b1 = 0.5( d - b)
const b2 = 0.5( d + b)
const m = 3.349e-26 # kg
const T = 2.5e-3 # K
const σv = sqrt(kB*T/m) #
const σ₀ = 10e-6 # 10 mkm #
const σz = 3e-4 # 0.3 mm # z
const σk = m*σv / (ħ*√3) # 2e8 m/s #
v₀ = zeros(3)
k₀ = zeros(3);: , , -, .
k
, . , , , . , , .
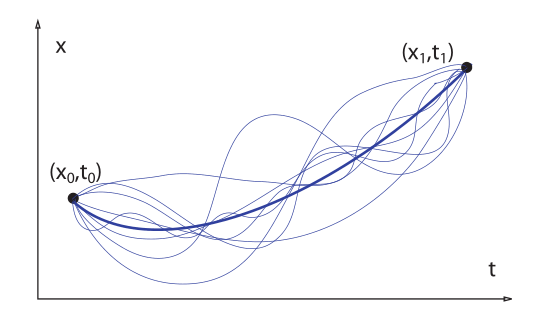
, . , , — . , , , . , , .
Quantum Mechanics And Path Integrals, A. R. Hibbs, R. P. Feynman, , 3.6 .
,
Z , . ,
, . , X, . :
, :
ε₀(t) = σ₀^2 + ( ħ/(2m*σ₀) * t )^2 + (ħ*t*σv/m)^2
s₀(t) = σ₀ + im*ħ/(2m*σ₀) * t
ρₓ(x, t) = exp( -x^2 / (2ε₀(t)) ) / sqrt( 2π*ε₀(t) )
t₁(v, z) = sqrt( 2*(l1-z)/g + (v/g)^2 ) - v/g
tf1 = t₁(v₀[3], 0) # s #
X1 = range(-100, stop = 100, length = 100)*1e-6
Z1 = range(0, stop = l1, length = 100)
Cron1 = range(0, stop = tf1, length = 100)
P1 = [ ρₓ(x, t) for t in Cron1, x in X1 ]
P1 /= maximum(P1); #
@gp "set title 'Wavefun before the slits'" xlab="Z, mkm" ylab="X, mkm"
@gp :- 1000Z1 1000000X1 P1 "w image notit"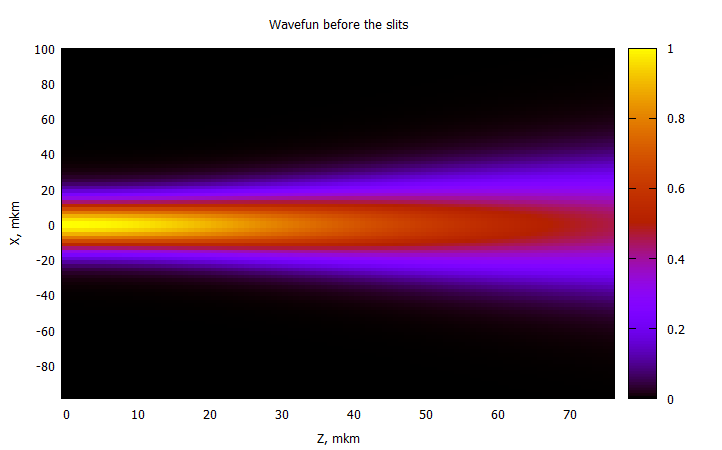
— .
, :
, :
function ρₓ(xᵢ, tᵢ)
Kₓ(xb, tb, xa, ta) = sqrt( m/(2im*π*ħ*(tb-ta)) ) * exp( im*m*(xb-xa)^2 / (2ħ*(tb-ta)) )
function subintrho(k)
ψₓ(x, t) = ( 2π*s₀(t) )^-0.25 * exp( -(x-ħ*k*t/m)^2 / (4σ₀*s₀(t)) + im*k*(x-ħ*k*t/m) )
subintpsi(x) = Kₓ(xᵢ, tᵢ, x, tf1) * ψₓ(x, tf1)
ψa = trapez(subintpsi, a1, a2, 200)
ψb = trapez(subintpsi, b1, b2, 200)
exp( -k^2 / (2σv^2) ) * abs2(ψa + ψb)
end
trapez(subintrho, -10σk, 10σk, 20) / sqrt( 2π*σv^2 )
endt₂(v, z) = sqrt( 2*(l1+l2-z)/g + (v/g)^2 ) - v/g
tf2 = t₂(v₀[3], 0) # s #
X2 = range(-800, stop = 800, length = 200)*1e-6
Z2 = range(l1, stop = l2, length = 100)
Cron2 = range(tf1, stop = tf2, length = 100)
@time P2 = [ ρₓ(x, t) for t in Cron2, x in X2 ];
P2 /= maximum(P2[4:end,:]);
@gp "set title 'Wavefun after the slits'" xlab="t, s" ylab="X, mkm"
@gp :- Cron2[4:end] 1000000X2 P2[4:end,:] "w image notit"2 :
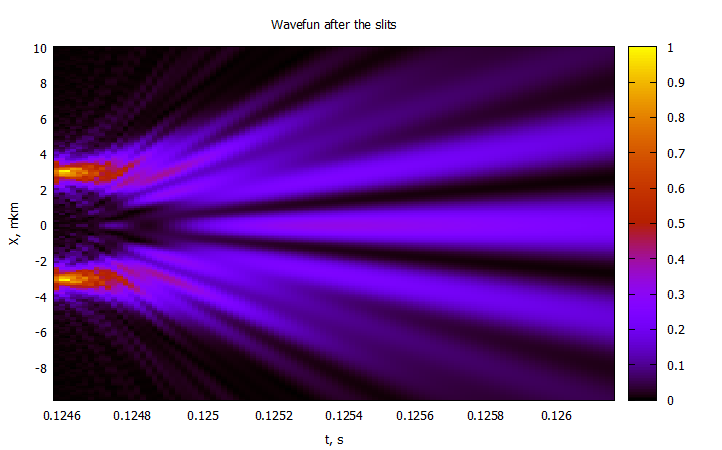
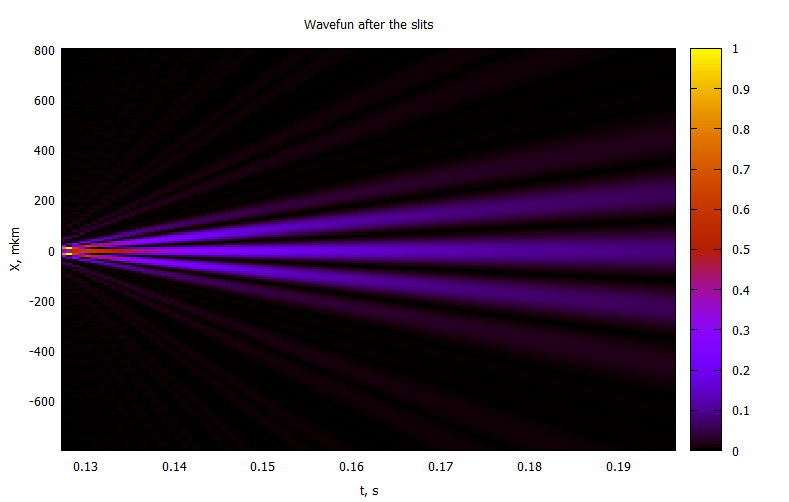
:
. . , ,
, ,
function xbs(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
#sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * cosϕt
end
@gp "set title 'Trajectories before slits'" xlab="t, s" ylab="X, mkm" # "set yrange [-10:10]"
@time for i in 1:80
x0 = randn()*σ₀
y0 = randn()*σ₀
v0 = randn()*σv*1e-4
prtclᵢ = [ xbs(t,x0,y0,v0) for t in Cron1 ]
@gp :- Cron1 1000000prtclᵢ "with lines notit lw 2 lc rgb 'black'"
# slits -4-> -2, 2->4 mkm
end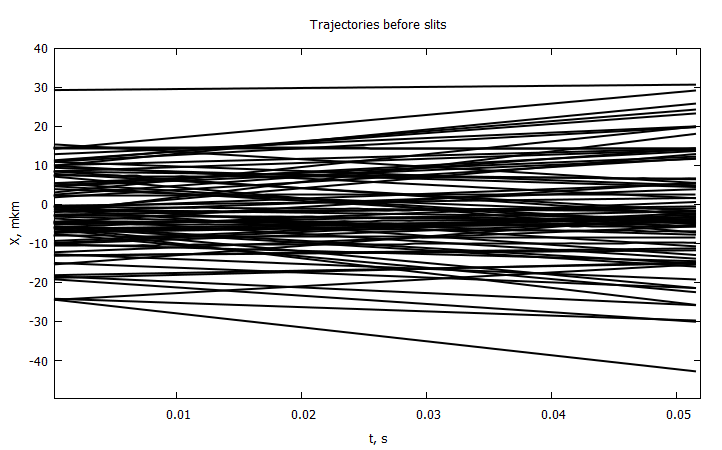
, , , , , . . . , .
Y , , . X . .
" " ,
function Uₓ(t, x)
γ = -m*x / ( ħ*(t-tf1) )
β = m/(2ħ) * ( 1/(t-tf1) + 1 / ( tf1*( 1 + (2m*σ₀^2 / (ħ*tf1) )^2 ) ) )
α = -( 4σ₀^2 * ( 1 + ( ħ*tf1 / (2m*σ₀^2) )^2 ) )^-1
f(x, u, t) = exp( ( α + im*β )*u^2 + im*γ*u )
C = f(x, a2, t) - f(x, a1, t) + f(x, b2, t) - f(x, b1, t)
H = trapez( u-> f(x, u, t) , a1, a2, 400) + trapez( u-> f(x, u, t) , b1, b2, 400)
return 1/(t-tf1) * ( x - 0.5/(α^2 + β^2) * ( β*imag(C/H) + α*real(C/H) - β*γ ) )
end
init() = bitrand()[1] ? rand()*(b2 - b1) + b1 : rand()*(a2 - a1) + a1
myrng(a, b, N) = collect( range(a, stop = b, length = N ÷ 2) )
n = 1
xx = 0
ξ = 1e-5
while xx < Cron2[end]-Cron2[1]
n+=1
xx += (ξ*n)^2
end
n
steps = [ (ξ*i)^2 for i in 1:n1 ]
Cronadapt = accumulate(+, steps, init = Cron2[1] )
function modelsolver(Np = 10, Nt = 100)
#xo = [ init() for i = 1:Np ] #
xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) ) #
xpath = zeros(Nt, Np)
xpath[1,:] = xo
for i in 2:Nt, j in 1:Np
xpath[i,j] = rk4(Uₓ, Cronadapt[i], xpath[i-1,j], steps[i] )
end
xpath
end@time paths = modelsolver(20, n);
@gp "set title 'Trajectories after the slits'" xlab="t, s" ylab="X, mkm" "set yrange [-800:800]"
for i in 1:size(paths, 2)
@gp :- Cronadapt 1e6paths[:,i] "with lines notit lw 1 lc rgb 'black'"
end- 4 , . 2
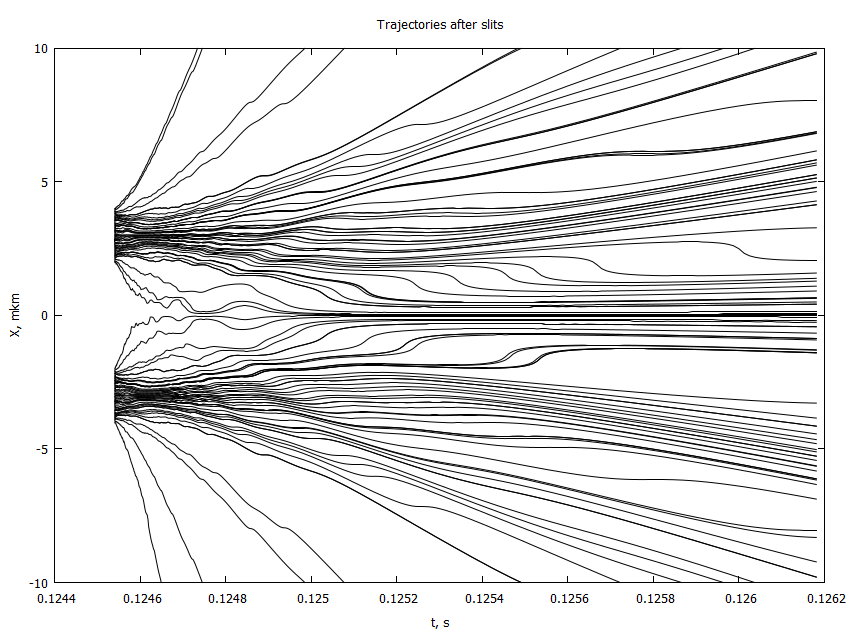
, : , , .
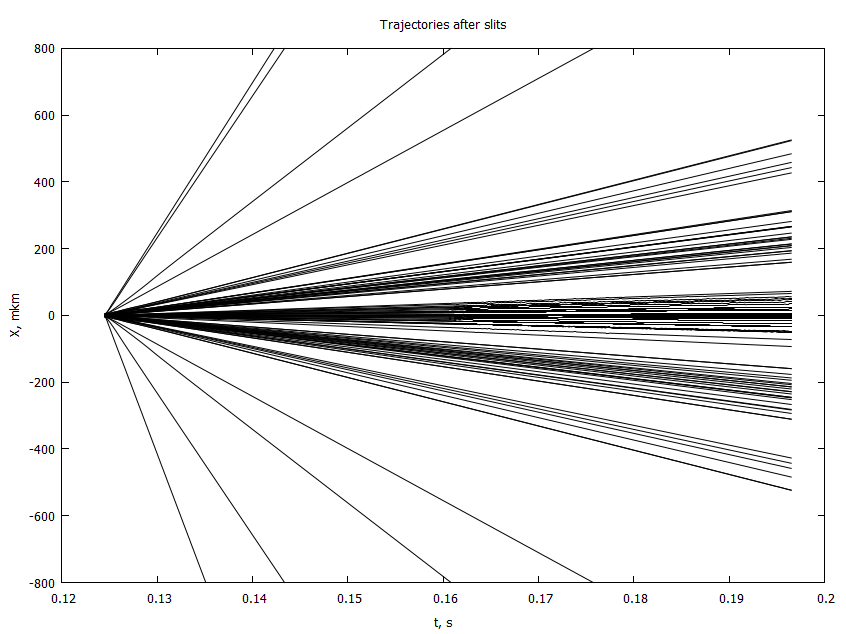
. , ,
function yas(t, xo, yo, vo)
cosϕ = xo / sqrt( xo^2 + yo^2 )
sinϕ = yo / sqrt( xo^2 + yo^2 )
atnx = -ħ*t / (2m*σ₀^2)
sinatnx = atnx / sqrt( atnx^2 + 1)
cosatnx = 1 / sqrt( atnx^2 + 1)
#cosϕt = cosϕ * cosatnx - sinϕ * sinatnx
sinϕt = sinϕ*cosatnx + cosϕ*sinatnx
σ₀t = sqrt( σ₀^2 + ( ħ*t / (2*m*σ₀) )^2 )
vo*t + sqrt(xo^2 + yo^2) * σ₀t/σ₀ * sinϕt
end
function modelsolver2(Np = 10)
Nt = length(Cronadapt)
xo = [ init() for i = 1:Np ]
#xo = vcat( myrng(a2, a1, Np), myrng(b1, b2, Np) )
xcoord = copy(xo)
ycoord = zeros(Np)
for i in 2:Nt, j in 1:Np
xcoord[j] = rk4(Uₓ, Cronadapt[i], xcoord[j], steps[i] )
end
for (i, x) in enumerate(xo)
y0 = randn()*yh
v0 = 0 #randn()*σv*1e-4
ycoord[i] = yas(Cronadapt[end], x, y0, v0)
end
xcoord, ycoord
end
@time X, Y = modelsolver2(100);
@gp "set title 'Impacts on the screen'" xlab="X, mm" ylab="Y, mm"# "set xrange [-1:1]"
@gp :- 1000X 1000Y "with points notit pt 7 ps 0.5 lc rgb 'black'"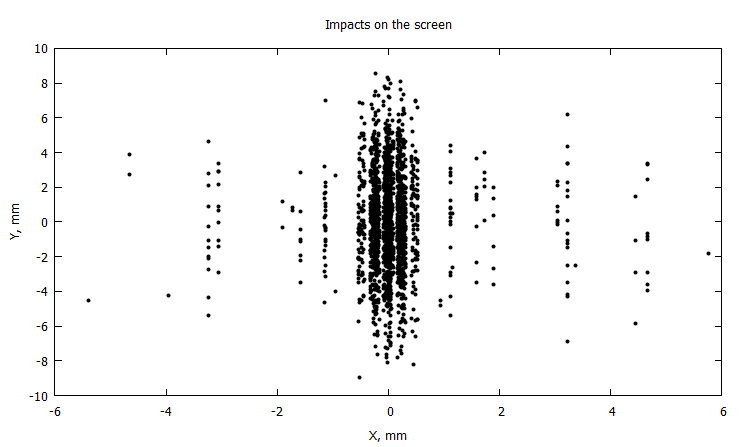
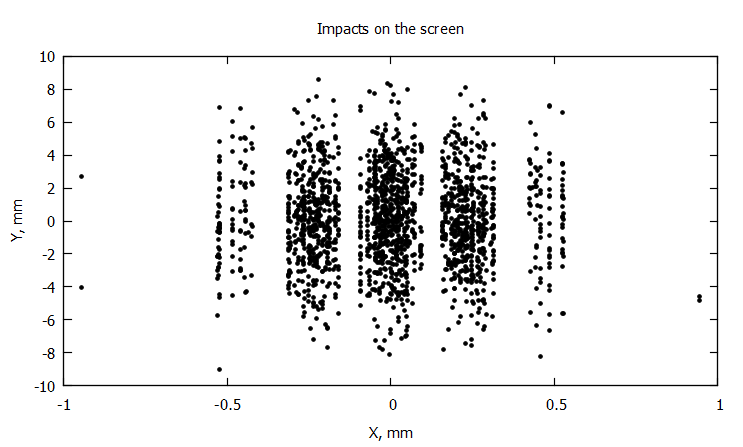
, , . , ,
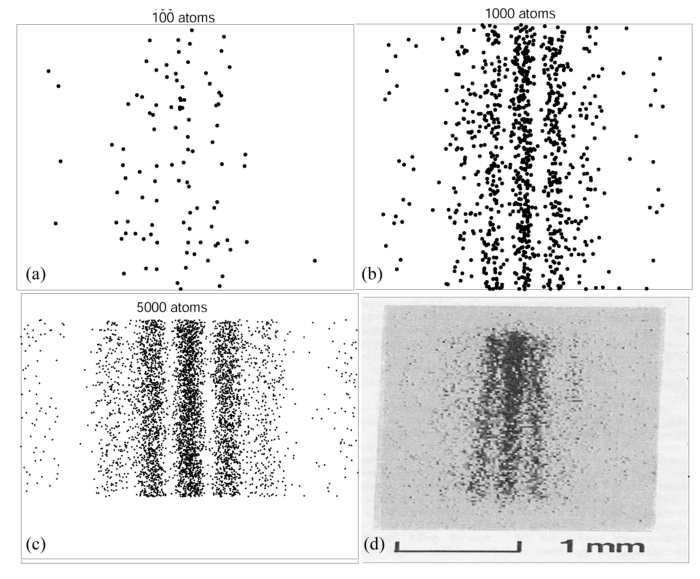
, , , , , — , .
- Measurement in the de Broglie-Bohm interpretation: Double-slit, Stern-Gerlach and EPR-B —
- — : , - - — ..